算数の指導で気になること
算数はつまずいたところまで遡って学習することが大切だとよくいわれますが、計算全般が苦手だという場合、何から学習し直せばいいのでしょうか。
計算が苦手な子にとって、苦手のきっかけを作った可能性が高いものとして『くり上がりのあるたし算』があります。小学1年生の2学期に学習しますが、これが“正しく”身についていないと、この先ずっと計算が苦手な子どもになってしまいかねません。
「計算ミスが多い」あるいは「計算ができないわけじゃないけど時間がかかる」という子は、たし算やひき算をするときに指を使って数えているケーもみられます。
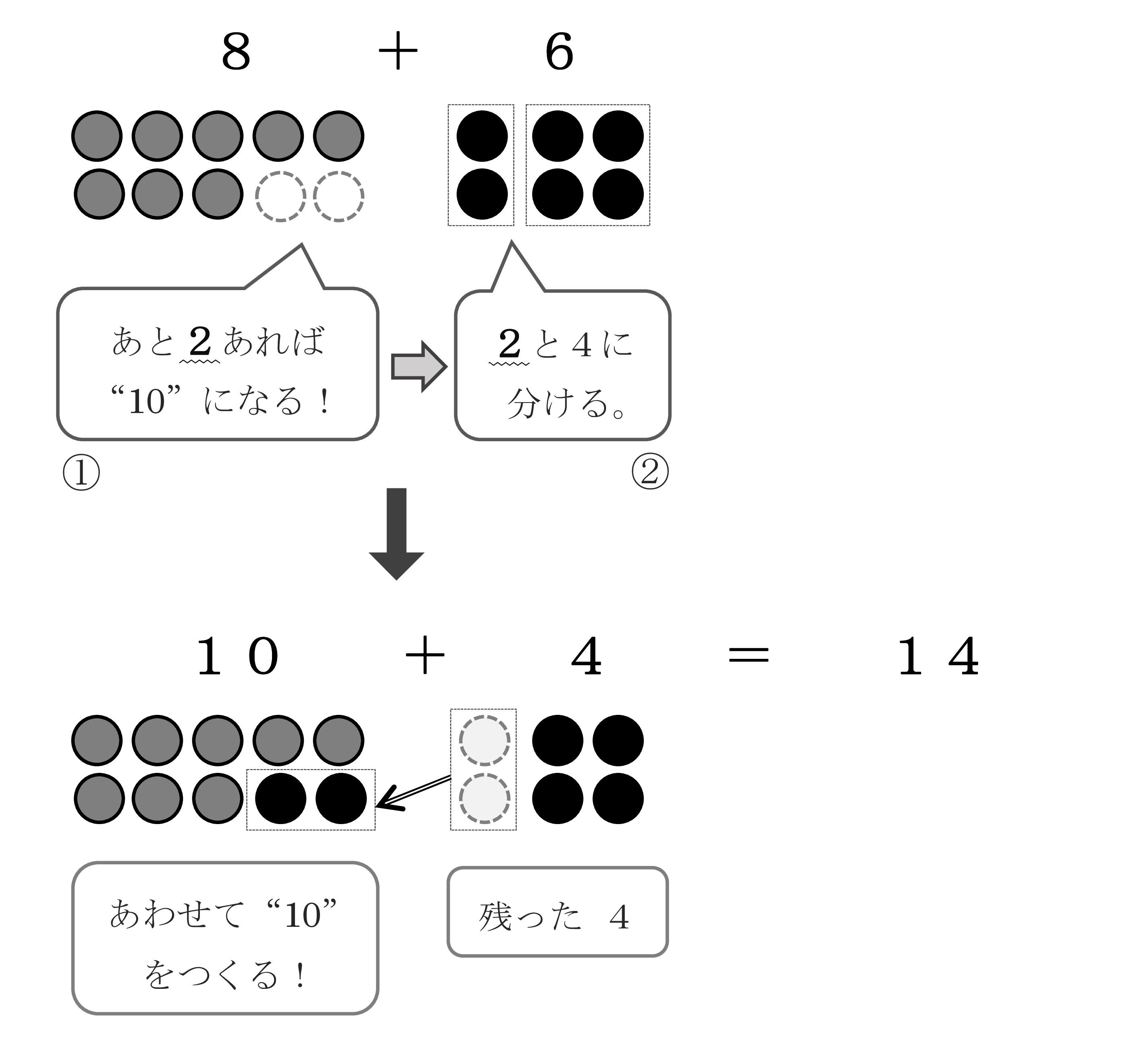
例えば、8+6 の計算。
指を折りながら(もしくは指は折らずとも)「8。・・・9、10、11、12、13、14。答えは14。」と、8の続きから6つ数えて答えを求めるやり方です。この方法は、時間がかかるばかりか、数えまちがえて不正解になることも少なくありません。
一方、くり上がりのあるたし算をきちんと身につけている子は、次のように考えて答えを求めています。
数の分解と合成の重要性
ここで、くり上がりのあるたし算をするときにポイントとなるのが、「あといくつで“10”になるのか考えつく」こと(上図①)と「1つの数を2つの数に分ける」こと(上図②)です。つまり、「数を分解」して「10を合成」する力です。
数の分解や合成は、くり上がりのあるたし算のほか、くり下がりのあるひき算や かけ算・わり算の筆算においても必要な思考です。そのため、ここをなおざりにすると様々な計算問題で苦しむことになるのです。
ですから、子どもが計算している過程をよく観察し、数の分解や合成が身についていないと感じたら、6+▢=10 や 8=▢+3 などの▢にあてはまる数を考える問題を徹底して練習させましょう。特に『たして10』になる組み合わせは重点的に、9とおり全て覚えてしまうくらい練習してほしいのです。
分数の「約分力」で差が出ます
「数の分解」ではもうひとつ、かけ算の式に分解する力も重要です。
「九九は完璧だけどわり算に時間がかかる」あるいは「分数のかけ算・わり算でいつも約分を見落としてしまう」という子、結構いると思います。
例えば、![]() の計算。
の計算。
6と15が「3で約分できる」ことに気づかずこのままかけ算をすると、
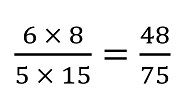
となり、48と75が「3で約分できる」ことを考えつくのは余計に難しくなってしまいます。
約分のできる子は
一方、式を見てすぐに約分できる子は、自然と次のようなことを考えています。
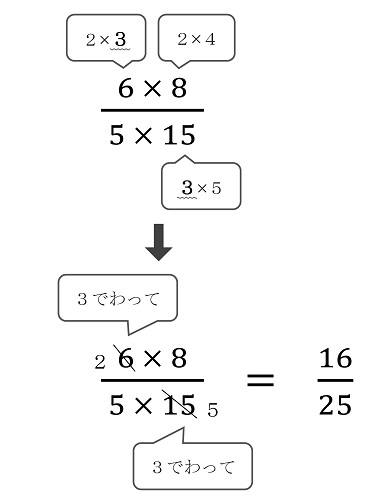
約分の際にポイントとなるのは、「数字を見てかけ算の式(九九)が思い浮かぶ」ことです。
約分力を鍛えるために
まずはかけ算九九が完璧であることが前提ですが、たし算に分解するのと同様、3×▢=21 や 18=2×▢/▢×6、慣れたら▢を増やして ▢×▢=21 や 18=▢×▢(2パターン) といった問題をとことん練習します。これがスラスラとできるようになると、約数・公約数を素早く見つけられたり、「比」の習得もスムーズになるはずです。
分解と合成は応用問題にも対応します
数を自由に分解・合成することができるようになると、計算力が上がるだけでなく、図形やグラフを描くのが上手になったり、応用問題に対し考える筋道を立てることにも役立ちます。
学指会では、色々な角度から“数”を見る方法を身につけさせ、子どもたちの思考力・活用力を養っていきます。
(算数担当:カネタカ)









